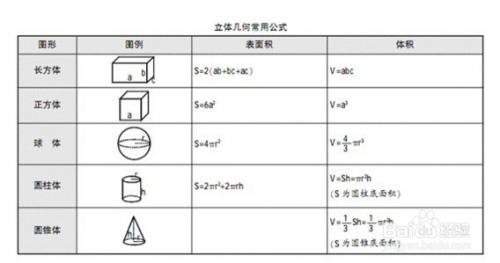
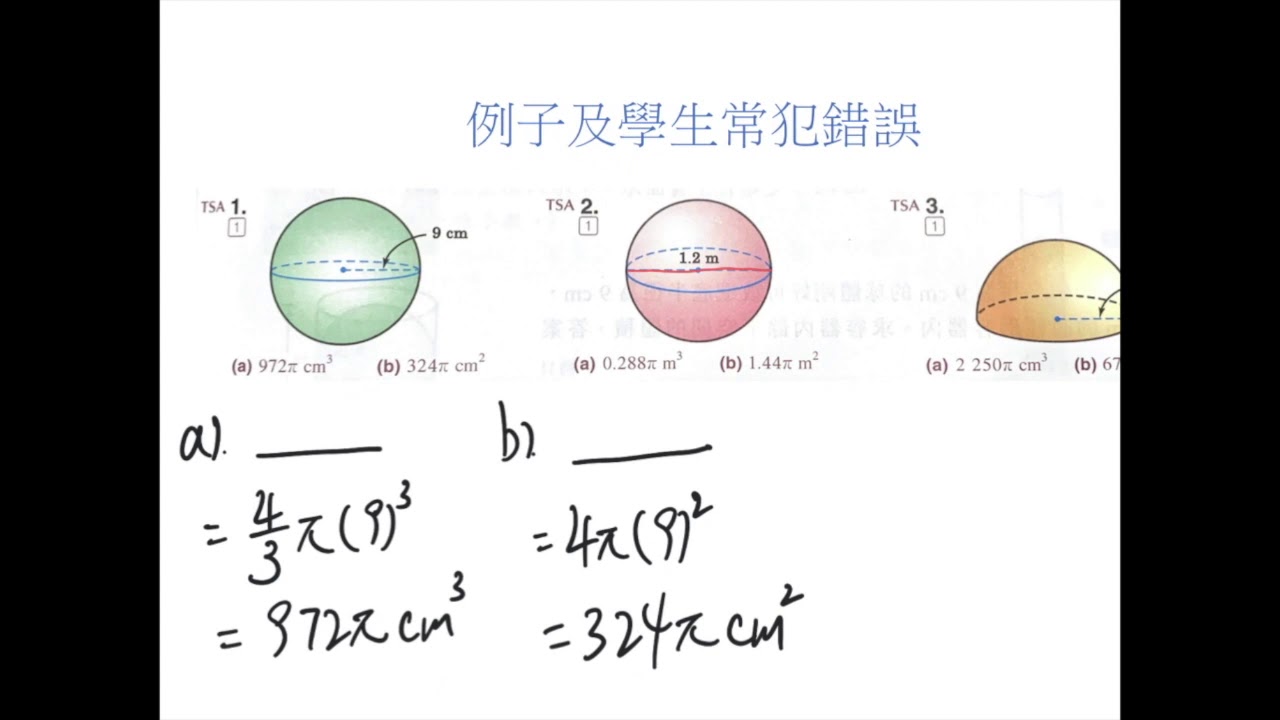
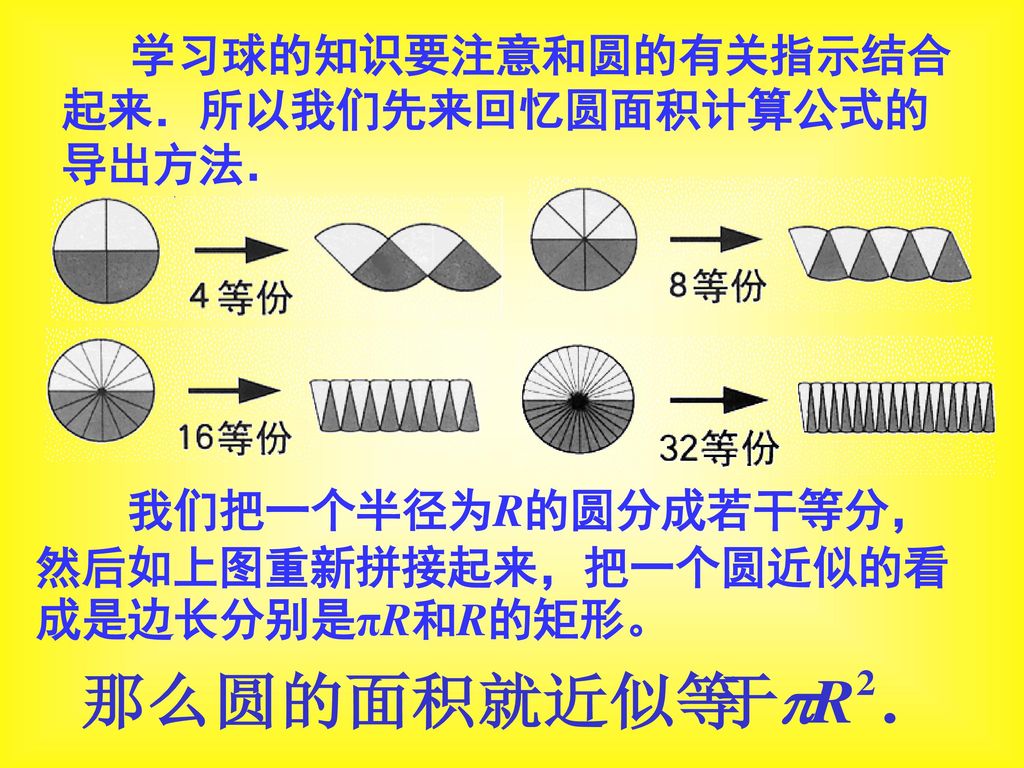
半球の表面積 S =球の表面積の半分+半球の切り口である直径4cm(半径2cm)の円の面積であることから S = 4π × 22 × 1 2 + 22π = 8π + 4π = 12π 答え 12π cm² ~立体の体積・表面積を求める公式まとめ~ 立方体・直方体の体積の求め方 円柱の体積の求めV = 体積 S = 角錐底面積 角錐 角錐 pyramid V = 体積 S = 角錐底面積 角錐台 V = 体積 (角錐台) S1 = 角錐底面積 S2 = 角錐上面積 球体 V = 体積 A = 球体の表面積 r = 球体半径 楕円体 楕円体の体積 → 楕円体 楕円体の表面積 台形 A = 面積 A = 面積 ヘロンの公式 A = 面積 = bh/2 又は ヘロンの公式球の体積と表面積半径 \(r\) の球の体積と表面積を求める公式は以下のようになります。\(球の体積=\displaystyle \frac{4}{3}\pi r^3\)\(球の表面積=4\pi r^2\)「なぜこの公式が成立するのか」については中学生の知識の範囲外です。証明には高校数学の「積分」という知識が必要です。どうしても気に
球的体积公式和表面积公式 高三网
球 面積 体積 求め方
球 面積 体積 求め方- 球の表面積の求め方の公式を1発でおぼえる方法 球の表面積の求め方の公式である、 4×π×半径の二乗 を一発で暗記してできちゃう語呂を紹介しよう。 このイメージさえ掴んじまえば、テストでも公式を忘れないはず! 球の表面積の公式を暗記するためS:球の表面積と同じ。 T:そうすると、高さはrで同じだから、三角錐の体積=底面積×高さ×(1/3)だから、それの合計は球の体積になる。 つまり、球の面積×高さ×(1/3)=球の面積×r×(1/3)=4(πr 3 )/3 S:だから、球の表面積=(4(πr 3 )/3




用微积分解答半径为a的球的表面积 雨露学习互助
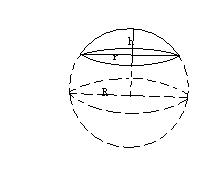
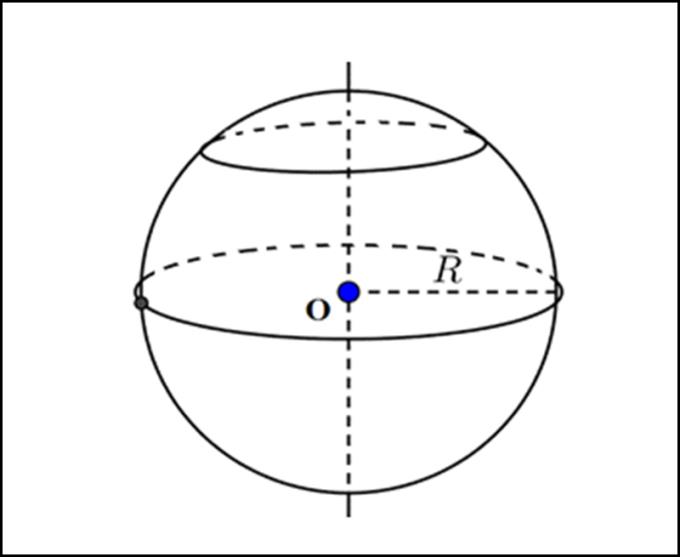
球の表面積と体積 ここでは、球の表面積と体積を求める公式を紹介しましょう。 表面積 まずは表面積です。 球の半径をr、円周率をπ、求める球の表面積をSとすると これが球の表面積を求める公式です。 体積 続いて体積です。 球の半まずは、「球の体積」と「球の表面積」を計算する公式の確認をしましょう。 球の体積 半径\(r\)の球の体積\(V\)は $$V = \frac{4}{3} \pi r^3$$ で与えられます(\(\pi\)は円周率) 球の表面積 半径\(r\)の球の表面積を\(S\)は $$S = 4 \pi r^2$$ で与えられます(\(\pi\)は円周率)。円周長から体積 L 体積 球 球 半球 中空球 円周から体積 円柱 円柱 パイプ 円周から体積 立方体 立方体・直方体 角パイプ 錐体 円すい 四角すい 多角形 6角柱 六角柱 その他 断面積から
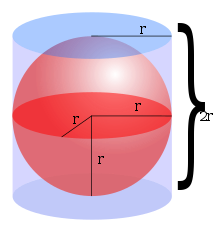
球 ボール 体積計算 公式 求め方 計算方法 直径 半径 自動 円周率 volume51 7 立体の体積と表面積 150 半径 3 cmの球と,その球がちょうど入る円柱,その円柱に ちょうど入る円錐がある。このとき,次の問いに答えよ。 ⑴ 球と円柱と円錐の体積の比を「球:円柱:円錐」と 球の体積と表面積の公式について まずは証明の前に,球の表面積と体積に関して認識しておくべきことを整理しておきました。 以下の語呂合わせで覚える方法が有名です: 球の表面積: 4 π r 2 4\pi r^2 4 π r 2 →「心配アール二乗」 球の体積: 4 3 π r 3 \dfrac{4}{3}\pi r^3 3 4 π r 3 →「身の上に心配アール三乗」
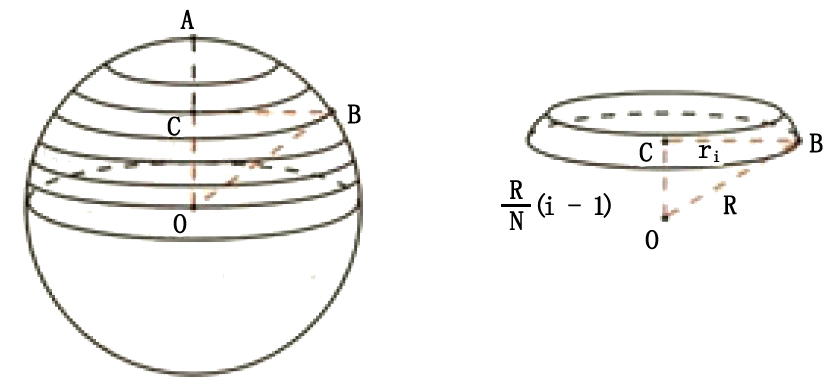
球の体積・表面積 組 番 名前 学習日 月 日 6cm 6cm Title 算数オリエンテーション 名前( ) Author 諏訪部 真紀 Created Date AM 円柱の側面積=球 の表面積 を示すことによって, (円柱の側面積= なので,) 球体の表面積= を示すことができます. 輪切りの考え方 円柱と球を真横に並べる. 自分の好きな高さで輪切りにする. 輪切りされた部分の表面積(赤色)が等しいことを確かめる. どの位置で輪切りにしてもこのとき、球殻の体積は、(半径 r r の球の表面積 S)× Δr Δ r で求められるのです‼(← ここがポイント!



球缺体积公式 推导球缺的体积公式 尚书坊
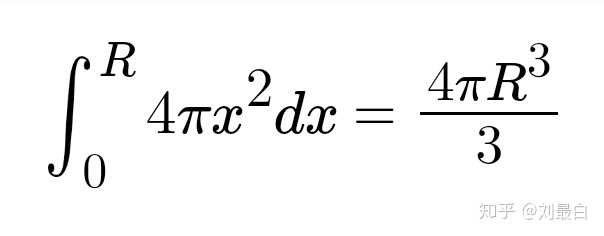



为什么计算圆的周长与面积 球的表面积与体积 使用的都是p 而不是三个不同的数 是偶然还是必然 知乎
円周長から体積計算 球 公式 求め方 ボール 自動 volume 体積 球 面積;面積が大きいか、またどのようにして考えるか をたずねた。生徒の反応としては、「 辺の長さを 測る。」 という意見が出た。そこで、球の体積の 公式が最初に示されたときには、現在のように 長さの単位は定められていなかったことを説明球の表面積の公式の求め方について考察する前段階として、球の体積の公式の求め方を 考察しておこう。下の図1において、球の中心から距離 x の点で切った断面である円の半径は √(r 2 -x 2) であるから、円の面積は、S(x)=π(r 2 -x 2) となる。 よって



为什么对球的体积公式求导就是球的面积公式




球の体積と表面積の公式をごちゃまぜにしない2つのポイント Qikeru 学びを楽しくわかりやすく
313 体積の計算 次314 曲面積上3 多重積分前312 演習問題 ~ 多重積分の積分変数の変換 313体積の計算 例 363(球の体積) 半径 の球の体積は である. これを多重積分で求める. (その 1) 球を 8 等分し底面が であり,上面が の体積 として求める.2 次元の極座標 , とおくと,領域 と等価な領域直円錐の体積 斜切円錐の体積 一部が欠けた直円錐の体積 円錐台の体積 楕円錐の体積 楕円錐台の体積 球の体積 一部が欠けた球の体積 弓形の回転体の体積 一部が欠けた弓形の回転体の体積 半球台の体積 円環体の体積 楕円体の体積 一部が欠けた楕円体の体積体積の大きさ(5:11)に引きずられて、計算で求めるまで同じになることが気付けませんでし た。従って、球のリンゴの直径をn等分した各物体の皮の表面積は全部同じ値を持つんです ね。 カルピスさんからのコメントです。(令和3年3月29日付け) 円の場合も同じように考えて良いですか?円の



圆球表面积 球体表面积的公式证明 篆体字转换器




球の体積と表面積 Youtube
球の表面積と体積1 名前 次の式を書きなさい。 3# ①半径 の球の体積 を求める式。 4# ②半径 の球の表面積 を求める式。 32 次の球の表面積と体積を求めなさい。 cm 表面積: 体積: cm 表面積: 体積: 右の図は、半径が cmの球を、中心を通る平面で切って できた立体である。このとき次の 問い V = 4 3π(3r2dr 3rdr2 dr3) = 4πr2dr 結局この値は円の表面積 4πr2 を底面とし、球殻の厚さ dr を高さとする直方体の体積と等しい。球の体積や表面積の公式 今回は 「球の体積や表面積」 について学習しよう。 球は2つの公式を覚えてしまえば、それでおしまい! point 問題を解いて、2つの公式に慣れていこう。 この授業の先生 今川 和哉 先生 どんなに数学がニガテな生徒でも「これだけ身につければ解ける」という超



悟空问答 为什么球体积公式对半径求导是球面积公式 而圆面积公式对半径求导又是圆周长公式 9个回答



面积体积计算软件下载 面积体积计算下载v1 0绿色免费版 多多软件站
球の表面積を 積分 = 球の体積 逆に、 円の面積を 微分 = 円周 球の体積を 微分 = 球の表面積 この関係が理解できたら、 公式丸暗記からは解放されて楽になりますね! 「積分」は、 無限に細く切った線を 足し合わせて面をつくる 半径 \(t\) の球の表面積を \(S(t)\) と書く。 三次元空間において、原点からの距離が \(t\) 以上 \(t \Delta t\) 以下の間にある部分(球殻)を考える。 \(\Delta t\) が十分小さいとき、この球殻の体積は \((\text{表面積}) \times (\text{厚さ}) = S(t) \, \Delta t\) とみなせる。球の表面積、体積の解答 直径 10 cm の球の半径は 5 cm なので、表面積は 4 π ⋅ 5 2 = 100 π ≒ 100 × 314 = 314 cm 2 よって、1辺 8 cm の立方体の表面積の方が大きい。 水中に入れた球の体積は 4 3 π ⋅ 3 3 = 36 π cm 3 なので、水の体積と球の体積の和は 10 ⋅ 10 ⋅ 9 36




球體表面積 球體表面積是指球面所圍成的幾何體的面積 它包括球面和球面所圍 華人百科



椭球 维基百科 自由的百科全书
今回は球の体積の何で?にお答えできればと存じます。 球の体積の公式のなぜ? 球の中心を とし、頂点を とする正四角錐で球を 等分していくことを考える。 このとき、 を無限に近づけていくと、四角錐の高さは球の半径 に限りなく等しくなる。また、球の表面積は 等分される。このとき人類はどうやって球の体積を求めたのか 1、アルキメデスは球の体積をどうやって見つけたの? T:球の体積は半径をrとすると、4/3・π・r 3 で求めることができるんです。覚え方は、『3分で忘れる心配あーるの参上。』『身の上に心配あーるのさんじょう。』単元「空間図形」の小単元「球の表面積と体積」(2時間)における数学的活動を取り入れた授業展開案です。 単元 空間図形 (啓林館) ・ g ・ 球の表面積と体積(移行措置に伴う補助教材) 全2時間



数学一分钟球的体积公式推导证明 哔哩哔哩 つロ干杯 Bilibili



在球的体积公式中 为什么会出现三分之四这个奇怪的系数 体积 公式 系数 新浪新闻
球の表面積 \LARGE {4\pi r^2} 半径4㎝の球の表面積 \large {4\pi \times 4^2} \large {=4\pi \times 16} \large {=64\pi (cm^2)} 公式を覚えることができたら r の部分に半径の値を当てはめてやるだけでOKです! 計算自体は簡単^^ 円の面積から球の体積を求め、さらに高次元球の体積と表面積を計算することによって微積分の概念を学習する。 文学と日常に学ぶ自然界のしくみ 後藤信行のブログ 大学の微積分:高次元球の体積と表面積 大学院入試過去問 Twitter Facebook はてブ Pocket LINE コピー 半径 の円




如何不用微积分算个球 网易订阅




用微积分解答半径为a的球的表面积 雨露学习互助




球冠面积 体积 牛客博客




球の体積と表面積 公式と計算問題と証明 Irohabook




如何找到球的面积和体积 数学21




圆锥与球与圆柱




如何计算球的体积 5 步骤




面积体积计算软件 面积体积计算软件下载v1 0 免费版 安下载




椭圆体 椭球体体积 表面积计算公式与在线计算器 三贝计算网 23bei Com



球体积怎么求公式 百度经验




012 球的体积空间几何体高中数学 Youtube



写给5年级的学生 球公式是如何推导出来的 表面积




14 平面及立體圖形 立體圖形的表面積及體積 齊齊溫




數學真魅 球體體積公式derivation Of Formula Of Volume Of Sphere



Q Tbn And9gcr4yydsanpcv9odoui8ies6cbemi 5dfwxzcqjdm Pjn0r0 Ymu Usqp Cau




球體表面積 球體表面積是指球面所圍成的幾何體的面積 它包括球面和球面所圍 華人百科




球 圆球 体体积 表面积 周长 质量在线计算器 三贝计算网 23bei Com



柱 锥 台 球的体积公式推导 不用积分 Li Hua 博客园




球的体积公式推导图文 如何用微积分知识推导球的体积公式 三人行教育网 Www 3rxing Org



球缺 维基百科 自由的百科全书



1



球冠体积计算公式附图 搜狗图片搜索




球面積積分球的體積 Itha



球体体积公式是球体体积公式是什么



球面 維基百科 自由的百科全書



球體的體積及表面面積 哔哩哔哩 Bilibili



球的面积和体积公式 西瓜视频搜索



球体面积公式是什么 球体公式 园球体表面积计算公式



球冠表面积计算公式 圣恩灵修网




球的表面积与体积 怎么用微积分证明球的表面积和体积公式 三人行教育网 Www 3rxing Org




C 计算圆周长面积 圆柱体积 圆球体积 Carujan的博客 程序员宅基地 C 求圆柱体体积 程序员宅基地



1



2



球的体积公式和表面积公式 高三网



球的表面积公式推导 万图壁纸网
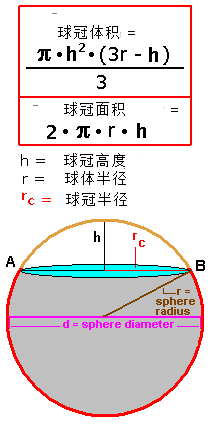



球冠在线计算器 在线计算 在线计算器 计算器在线计算




球表面積計算球的體積 Jlxpis



球的体积公式推导 孤云出岫 去留一无所系 朗镜悬空 静躁两不相干 Csdn博客 球的体积公式




球的體積求導便是球的表面積 互為逆運算 降維與升維 每日頭條




求球体的表面积和体积 修也 Csdn博客




球体积公式




科學月刊 大小有什麼差別 上




球冠体积的推导 Meloor的博客 Csdn博客 球冠体积




球冠 球缺的体积 面积 弧长 弦长在线计算器 三贝计算网 23bei Com



细品教材 从生活经验中我们知道 不能将橘子皮展成平面 因为橘子皮近似于球面 这种曲面不能展成平面图形 那么 人们又是怎样计算球面的面积的呢 古人在计算圆周率时 一般是用割圆术 即用圆的内接或外切正多边形来逼近圆的周长 理论上 只要圆内接正多边形边



高中数学牛x 公式 利用三棱锥内切球的半径与体积关系式快速解题 努力学习网



物理方法解决数学问题 二 Archimedes与球体积公式 Matrix67 The Aha Moments




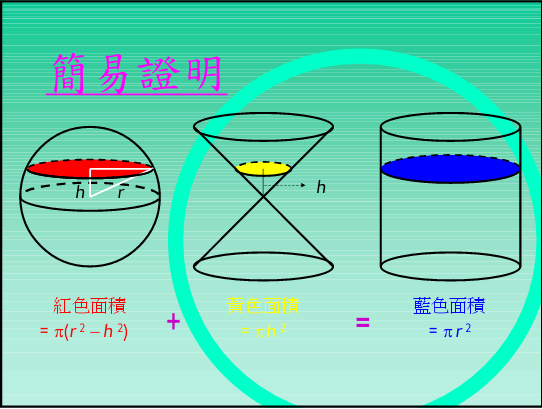
圆面积与球体积的统一探讨 参考网



球體體積 總表面面積 Youtube
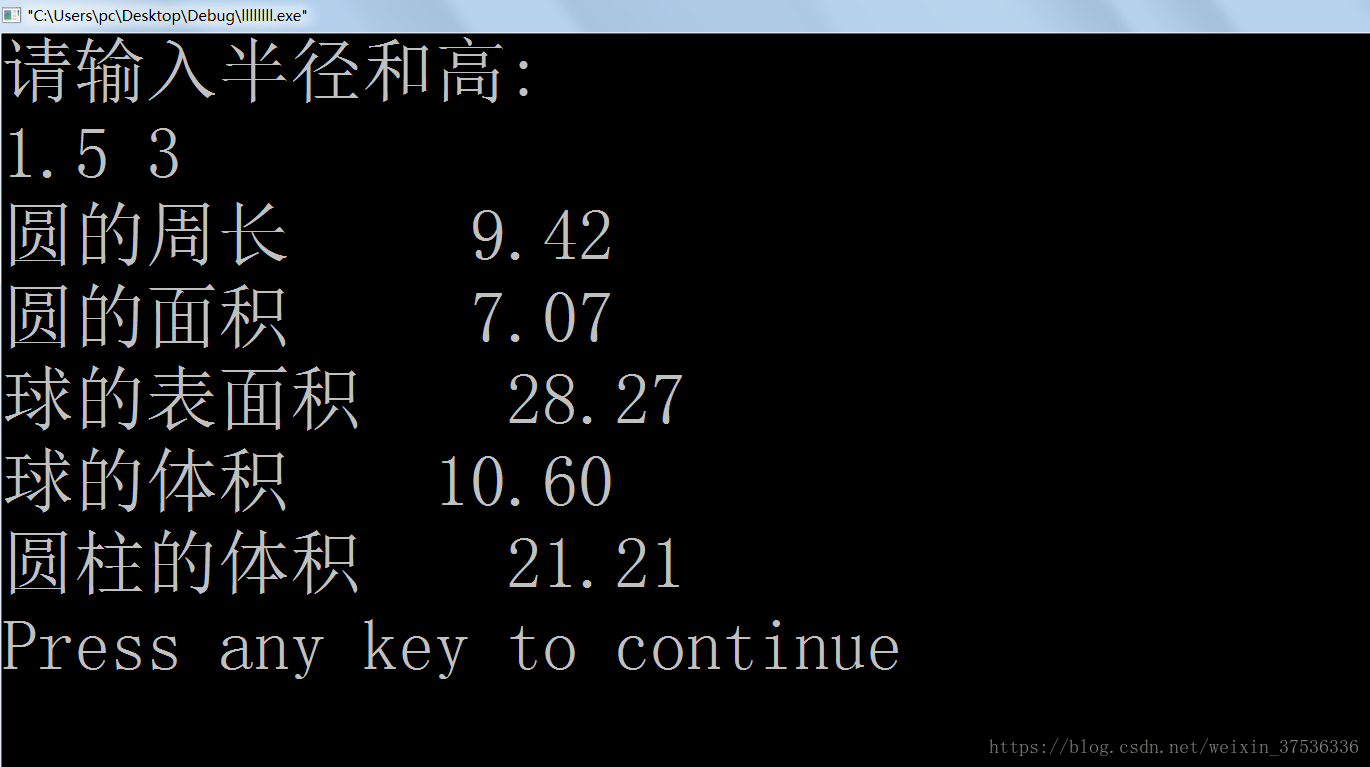



圆半径r 1 5 圆柱高h 3 求圆周长 圆面积 圆球表面积 圆球体积 圆柱体积 希望能对学习c语言的朋友有帮助 程序员宅基地




球表面積公式球體表面積 百度百科 Kmbymh




原 C 公式 计算球弧面体积 球缺 南水之源 博客园



高中数学必修2教案 1 3 2 球的体积和表面积 淘文库



計算球體面積的公式 球體面積是完整而準確的



球体积的前世今生 新华网




积分求圆球面积和体积下载 Word模板 爱问共享资料



1



球的体积求导便是球的表面积 互为逆运算 降维与升维 五四公社




球的表面积例题 球的表面积和体积公式是什么 三人行教育网 Www 3rxing Org



圆球表面积 球体表面积的公式证明 篆体字转换器




常用球缺的面积 体积 重心高度 斜边长度计算 细点设计




积分求圆球面积和体积 解析 下载 Word模板 爱问共享资料




用感覺理解球體表面積公式 Youtube



球体体积公式 怎样计算球体的体积




表面积公式球




體表面積表初中數學 幾何 面積與體積公式 Uhlwc



常用体积计算公式 电子工程世界



球的体积和表面积ppt Download




球の体積と表面積の公式と覚え方を一目でわかるように図を用いて解説します 練習問題付き 高校生向け受験応援メディア 受験のミカタ




球体表面积及体积的推导 每日头条




球的体积与表面积 简书




球帽球体积球楔比表面积 点公式png图片素材免费下载 图片编号 Png素材网



球的體積



球體表面積球體 表面積 體積 Vhjk



球冠体积公式推导 请问在不知道球半径的情况下 怎么计算球冠的面积和体积 图片上这种面积怎么算 三人行教育网 Www 3rxing Org




高中立體幾何 巧求空間幾何體的體積的三個方法 雪花新闻




球台球带体积 侧面积 表面积计算公式与在线计算器 三贝计算网 23bei Com




球扇形 球心角体 体积 表面积计算公式与在线计算器 三贝计算网 23bei Com



球冠体积 表面积在线计算器



多维球体的体积 小时百科




球表面積公式球體表面積 百度百科 Kmbymh



球的面积和体积公式 西瓜视频搜索



球的表面積的求法 中學數學課 隨意窩xuite日誌




面积体积计算软件 面积体积计算软件下载v1 0免费版 Pc6下载



球体体积公式推导图解 搜狗图片搜索



球冠面积 球缺体积 简书




中学数学 球の体積の求め方の公式を1発で覚える方法 Qikeru 学びを楽しくわかりやすく




高考数学考点之空间几何体的表面积和体积 王羽课堂
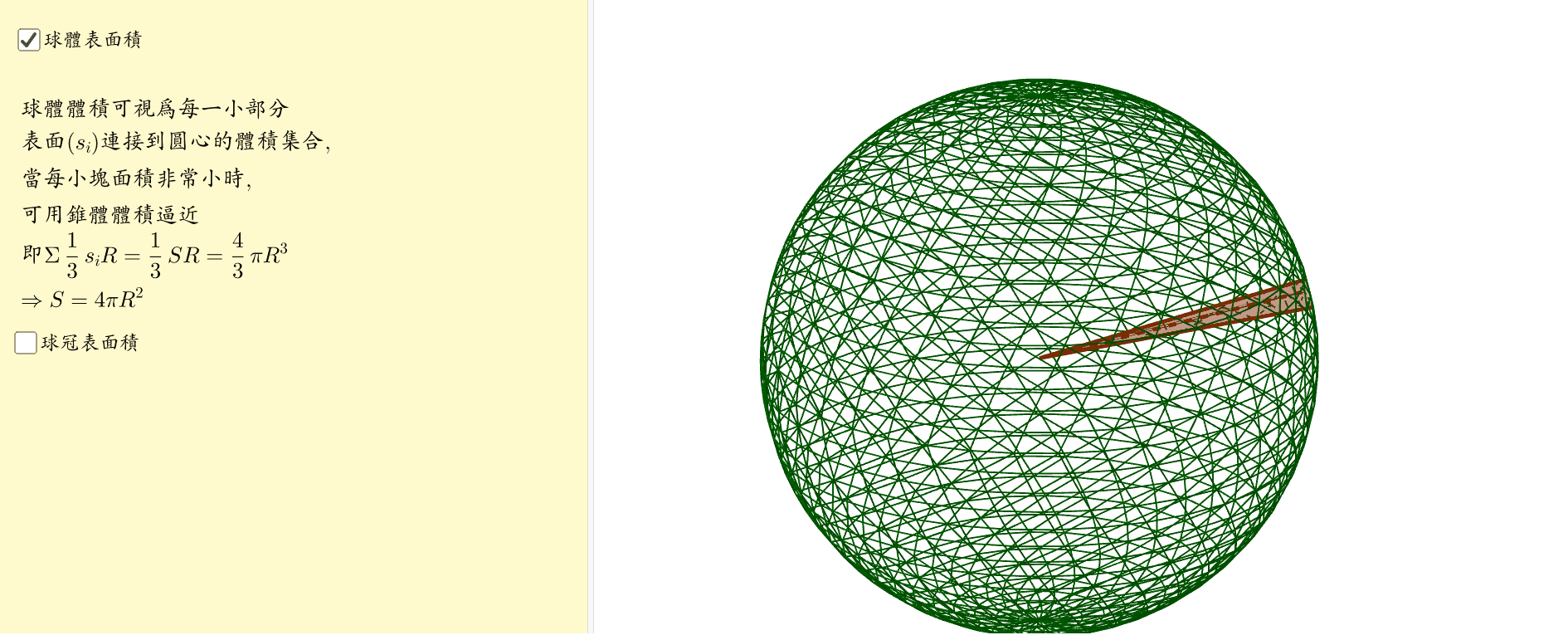



球體表面積 Geogebra



球面积体积公式原理 球的体积公式推导过程 公式学习



球的体积求导便是球的表面积 互为逆运算 降维与升维 五四公社



球的面积公式怎么算 球体体积面积公式是谁 公式学习



0 件のコメント:
コメントを投稿